

Note that if our matrix V is a non-singular matrix, we define our eigendecomposition as M = VΛV-1. We get a matrix that satisfies MV = VΛ with a diagonal matrix with eigenvalues and equivalent eigenvectors on matrix V’s columns. Use the eig() Function to Decompose Any Matrix Into Its Eigenvalues and Eigenvectors in MATLABĪ square matrix M has an eigenvalue (a scalar lambda λ) and an eigenvector as a non-zero vector A when they satisfy the equation MA = λA. Let us understand these concepts by looking at the following examples. The decomposition of any matrix into its eigenvalues and eigenvectors can be Cholesky decomposition or Hessenberg decomposition, etc., depending on our choice of requirements. We also call this decomposition matrix-diagonalization. We also use it to reduce the dimensions of our matrix to reduce the complexity. Note that an eigenfunction decomposes a matrix into its constituents. We will use different example codes and related outputs to clear your concepts and give you a complete insight into methods to decompose any matrix into its eigenvalues and eigenvectors in MATLAB.
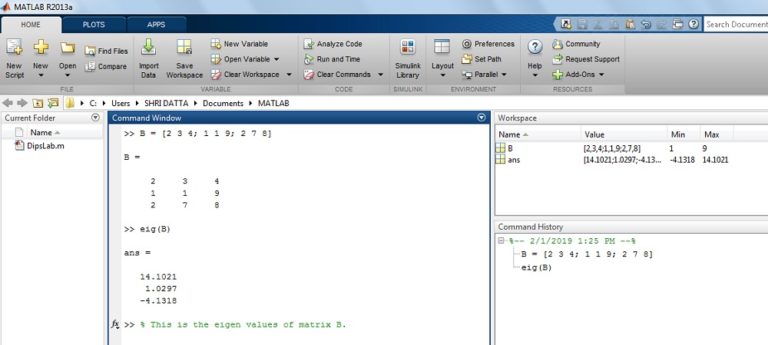
Eigenvalue Decomposition of a Matrix Into Its Eigenvalues and Eigenvectors in MATLAB We will look at different ways to decompose any matrix into its eigenvalues and eigenvectors in MATLAB. Use the eig() Function to Decompose Any Matrix Into Its Eigenvalues and Eigenvectors in MATLAB.Eigenvalue Decomposition of a Matrix Into Its Eigenvalues and Eigenvectors in MATLAB.


 0 kommentar(er)
0 kommentar(er)
